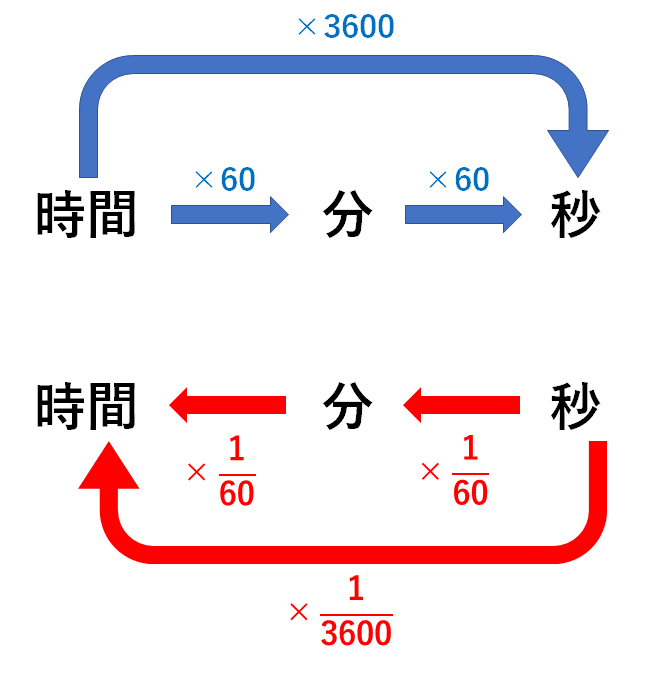
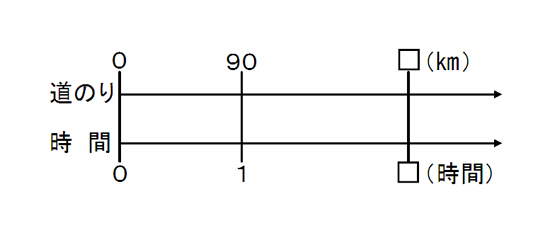
波の速さを表す式 v = \(\frac{λ}{T}\) = f λから、 v =50 Hz×40 m= m/s ですね。 図から波の速さを求めることもできますよ。 速さ=距離÷時間なので、波が1秒間に進む距離が分かれば良いわけです。 なので、波のどこか1点に注目して、その点が1秒間にどれだけの距離を移動するかこうして、進んだ距離が1kmだということを求めることができます。 速さの求め方 次は 「速さ」 です。 はじきの法則で確認すると、こちらになり② 速さを求める式 速さ = 道のり ÷ 時間 右の表は,こうじさん,ゆきさん,けん たさんが,家から学校まで走った時の道の りとかかった時間を表しています。3人の うち,だれが1番速く走ったかを考えます。 ② 3人の速さを求めましょう。 こうじさん (式) ゆきさん (式) けんたさん
音の速さの計算問題をくわしく解説
速さを求める式 物理
速さを求める式 物理->> 第4回 文字式の計算と1次方程式を解くこと 速さについて ;速さを求める式を確認する。 Q.1 P波が伝わる速さは何km/sか。 Q.2 S波が伝わる速さは何km/sか。 Q.3 地震の発生時刻は何時何分何秒か。 Q.4 地点Aの震源からの距離は何kmか。




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生
変位の式「s = 5t 3 3t 2 2t 9」において、t = 4のときの瞬間速度を求める この問題は、2次方程式が3次方程式になったことを除けば、パート1の例と同じであるため、同様の方法で解くことができます。 まずは、この式の導関数を求めます。 s = 5t 3 3t 2 2t 9速さの公式(道のり・時間) ホーム » 速さ » 速さの公式(道のり・時間) 速さ = 道のり ÷ 時間 道のり = 速さ × 時間 文字式の速さに関する問題について解説していきます。 割合と同様に苦手な人が多い単元なので、しっかりと理解を深めておきたいね! 割合(パーセント)の問題が苦手な人は こちらの記事も参考にしてみてくださいね^^
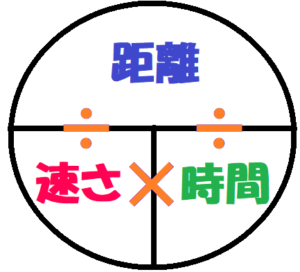
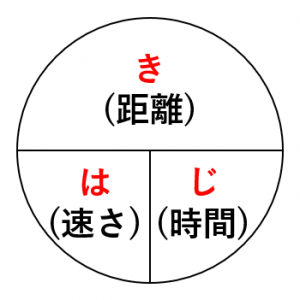
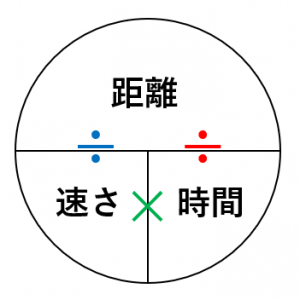
ベーシック数学 eテレ 毎週 月曜日 午後2:00〜2:10 ※この番組は、前年度の再放送A君の速さを\(x\) B君の速さを\(y\)とすると 反対方向に進む場合 A君の道のりは\(15x\)、B君の道のりは\(15y\)と表せます。 よって $$15x15y=3600$$ 同じ方向に進む場合 A君の道のりは\(30x\)、B君の道のりは\(30y\)と表せます。 よって $$30x30y=3600$$ 2つの式から連立速さが出てくる文字式の問題は、苦手の人が続出の危険地帯! 「速さ」を求めるには? 「時間」を求めるには? 「距離」を求めるには? それぞれの頭文字をとった「ハジキの法則」が成り立つのでしっかりおさえておこう。 point
速度式を用いて、瞬間の速さを求める \\begin{align} \color{red}{V}&=K・A \end{align} \ P o int!速さの表し方や比べ方について,単位量あたりの大きさの考えを基に数直線や式を用いて考え,表現 することができる。 (数学的な考え方) 速さに関わる数量の関係において,速さや道のり,時間を求めることができる。 (数量や図形についての技能)従って,長波の波速C は水深h のみで決まる(分散性のない波). 例題21の要点 分散関係を使って波の周期と水深から波長と波速を求める. 27 水粒子の運動速度と軌跡 速度ポテンシャルφが(211) 式のように求まっているので dx dt = u µ ≡− ∂φ ∂x




音の速さ 秒速でどれくらい 公式を確認しておこう 中学数学 理科の学習まとめサイト



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学
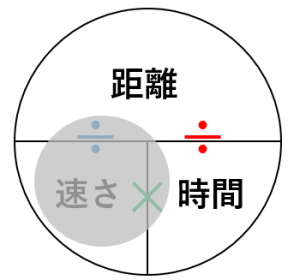
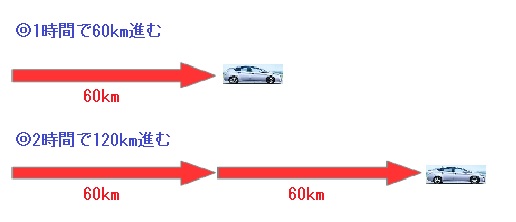
同じく速さを表すことができる。 時間と速さで距離をあらわす。 方程式というのは、 同じ数を=で結んで、 結果Xの値を求めていくので、 =の両側は同じ数、 いわゆる時間=時間 速さ=速さ 距離=距離 ということになります。 何度も、問題をやって速さを求める式を教えます 速さ=道のり÷時間 時速・分速・秒速 時速は、1時間あたりに進む道のり(㎞)で表した速さ 分速は、1分間あたりに進む道のり(m)で表した速さ 秒速は、1秒間あたりに進む道のり(mやcm)で表した速さ 赤い車の時速は60kmです。 青い車の時速は50kmです。 補足 これを公式として、まとめた音の速さを求める式がコレ! 音の速さを求める公式 $$音の速さ=\times (気温)$$ ゆい おっと難しそうな式が出てきたぞ いや、すっごくシンプルな公式だよ! ちょっと例題を見ておこう。 10℃における大気中の音の速さを求めましょう。 10℃を公式に



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学




速さと時間から道のりを求める問題 家庭学習レシピ
STEP2:等しい数量の関係をみつけ、方程式をつくる Aの歩いた距離 $$ Bの走った距離 $=$ 池の周りの距離 より、$\textcolor{blue}{80x170x=3000}$ STEP3:方程式の解を求める $80x170x=3000$ $\textcolor{blue}{x=12}$ STEP4:問題に適しているか確かめる水中では、およそ 秒速1500m の速さで音は進んで 波の速さと振動数が分かっている場合は、基本的な公式を用いて波長を求めることができます。特定の光子エネルギーを持つ光の波長を求めたいならば、光エネルギーの式を利用できます。正しい式を理解しさえすれば、波長の計算は簡単 一定の定義式と速度式を使った、入試で頻出の計算パターンがある。上の3STEPに基づいて解説していこう。 問題 A→2B+Cの反応が起こるとする。 一定温度でAの濃度を測定すると下図のようになった。 t(s) A(mol/L) 0




小学6年生の算数の速さのまとめ みけねこ小学校




6年生算数ドリル 速さ
速さに関する問題は、いろいろなパターンがあります。 基本一次方程式の利用(速さ) でも一部を見ましたが、ここでは、途中で速さが変わる問題を考えます。 ここでも、使うものは 速さ × 時間 = 距離 という関係式です。 どのように使うかを連立方程式 速さ1 a町からb町を通ってc町まで60kmある。a町からb町まで毎時30kmですすみ、b町からc町まで毎時40kmで進んだら合計で1時間48分かかった。 a町からb町までとb町からc町までのそれぞれの道のりを求めよ。 求めるものは道のりなので、 a町からb町をxkm, b町からc町をykmとする。地震波の伝わる速さは、走時曲線の傾き(時間軸が縦軸なので正確にはこの逆数)からわかる。この3つの値から、不連続面までの深さ(d(km))を求めるのである。 結論は となる。 この式の求め方を



中3物理 速さの単位変換 中学理科 ポイントまとめと整理




小6 算数 小6 21 速さの表し方 基本編 Youtube
距離を求める式 距離=時間×速度 かかった時間:4時間 速度:時速30km → 4÷30=1 → 進んだ距離は1km 速度の問題例 3時間に180km進んだ車の速度は時速何kmでしょう? 180km÷3時間 = 1時間に60km進む = 時速60km 時速30kmで5時間進むと何km進みますか? 1時間に30km進むので 5時間×30km=150km 150km進む 時速40km 速さの問題は分数で求める 難易度の高い速さの問題では、割り切れない問題が出題されるおそれがあります。 「時間=距離÷速さ」で時間が割り切れない、などの場合です。 例えば、17㎞を時速3㎞で歩いた場合の時間、という例を考えてみましょう。この波長の式を用いて波長を計算する 波の波長を求めるには、波の速さをその振動数で割るだけです。波長の式は次の通りです。 = 波長は、通常ギリシャ文字の (ラムダ)で表されます。;



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学



6年生の算数 速さ 時間 距離の式をイメージで覚える 算数検定7級
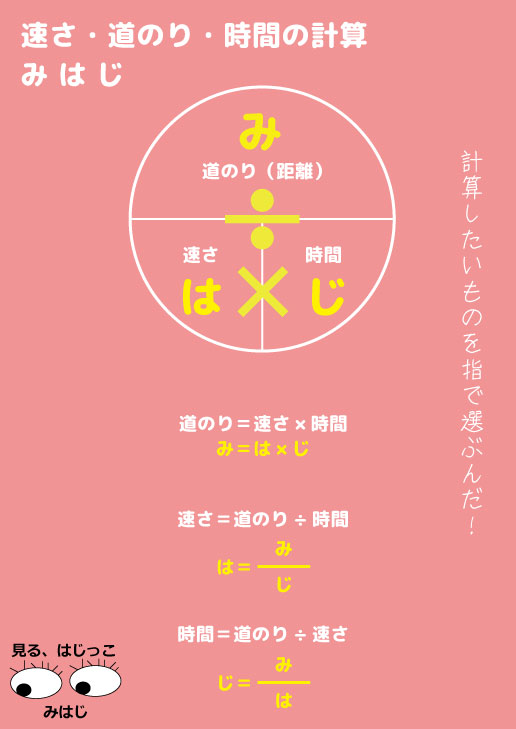
速さ、時間、道のりを求める3つの式をはじめに書くことにします。 問題は文章題の大問3つに取り組んでみましょう。 式や考え方を書きながら計算し、答えを求めましょう。 大問1は、このノート例では、45時間で何km進むかを先に考え、45時間を45分に直す、という手順で解いています。 45分は4・速さを求める公式を理解す る。 (エ)《観察・ノート》 第 4 時 ・速さと時間から、道のりを 求める。 数直線を用いて、式や数 値の意味を説明させ、理 解を深めさせる。 ・道のりの求め方を考えてい る。 (イ)《発言・ノート》 ・道のりを求める公式を理解す る。 (エ)《観察 はじきの法則をみると 「距離=速さ×時間」 なので、例題の計算式は次のようになります。 30km/h×4h=1km;



速さ 速さを表そう 第5学年 小学校 算数 My実践事例 日本文教出版



海図の問題を覚えよう 距離 速度 時間の計算
平均の速さと瞬間の速さって求める式一緒じゃないですか このふたつは何が違うのか教えてください 0 回答 ベストアンサー 8m 約1年前 「平均の速さ」は、「全体の移動距離(変位)」÷「その移動にかかった時間合計」。合計の時間でいくら進んだのか、の事です。 「瞬間の速さ」は、 中学数学の基本「一次方程式」。 方程式の「利用」や「応用」というかたちで、文章問題が出題される単元でもあります。 別の記事でご紹介した通り、文章問題は主に8種類。 初めて訪問してくれた皆さんのために



速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




時速や分速の計算でミスをしないために 分数の約分利用の徹底を 中学受験ナビ




等速直線運動 高校物理をあきらめる前に 高校物理をあきらめる前に




文字式 速さの問題をわかりやすく解く方法 数スタ
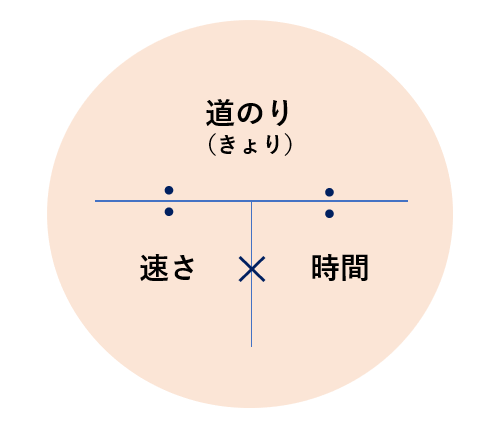



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社




平均の速さは変化の割合 傾き 永和進学ゼミ 個別指導ソフィア 学習塾ブログ
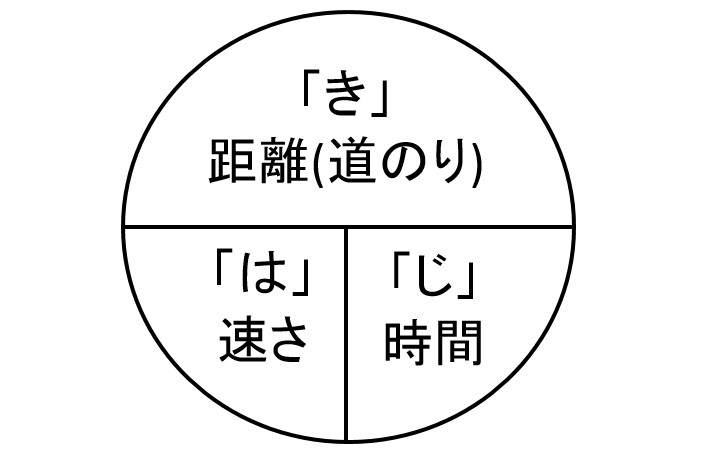



はじきの法則とは 距離 道のり 速さ 時間を計算する公式について とはとは Net




速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい
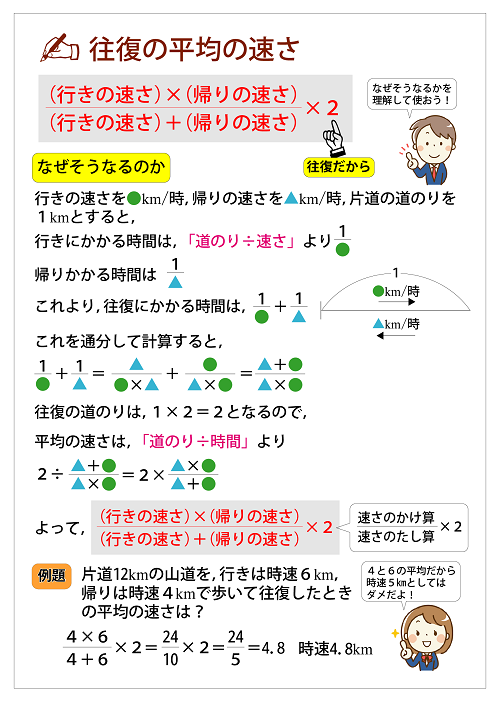



往復の平均の速さに関する公式のカードを作りました 恋する中高一貫校 適性検査 徹底攻略




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun
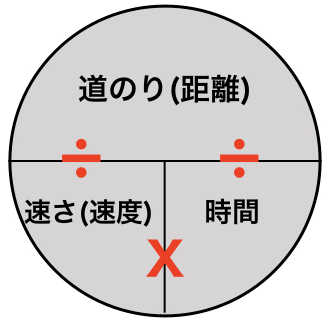



速度計算 速度 距離 時間と速さ 道のり 時間の覚え方攻略 Landgather
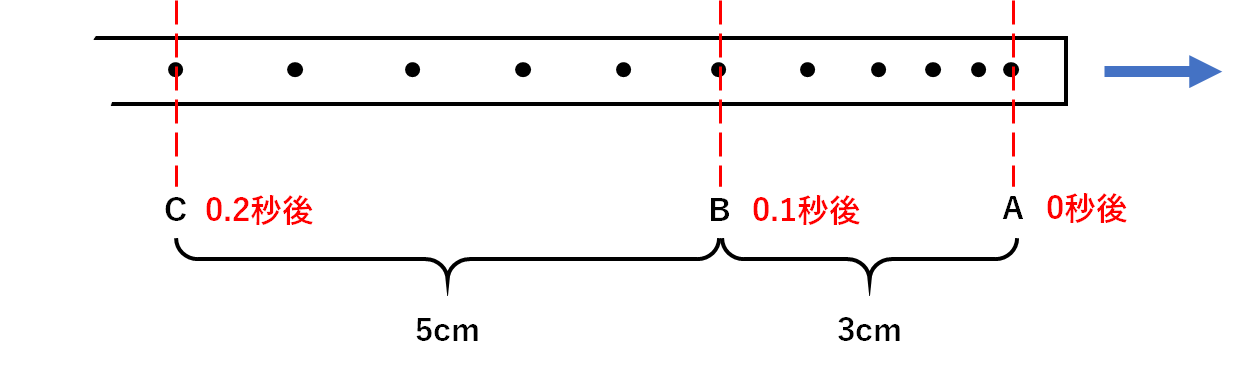



中3物理 瞬間の速さ 中学理科 ポイントまとめと整理




速さ 時間 距離 はじき みはじ の法則 小学生 中学生の無料学習プリント Yattoke 無料プリント




小学6年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




高校物理 波長 L m 振幅 a m 速さ v m s 映像授業のtry It トライイット



1




みんなの知識 ちょっと便利帳 ある距離を ある速度で進んだ時にかかる時間は 距離 速度 時間を計算する 移動した距離 時速 時間などを求める ことができます



小学生 算数 完全習得 速さの計算 こいがくぼ翼学習塾




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく



速さ 速さを表そう 第5学年 小学校 算数 My実践事例 日本文教出版
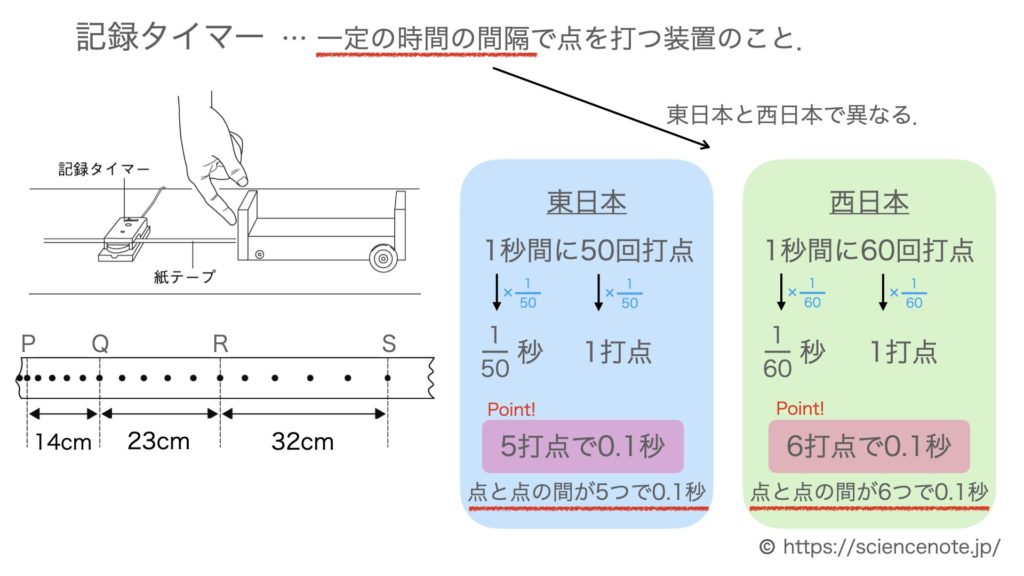



記録タイマーを使った物体の平均の速さの求め方 Hiromaru Note



1
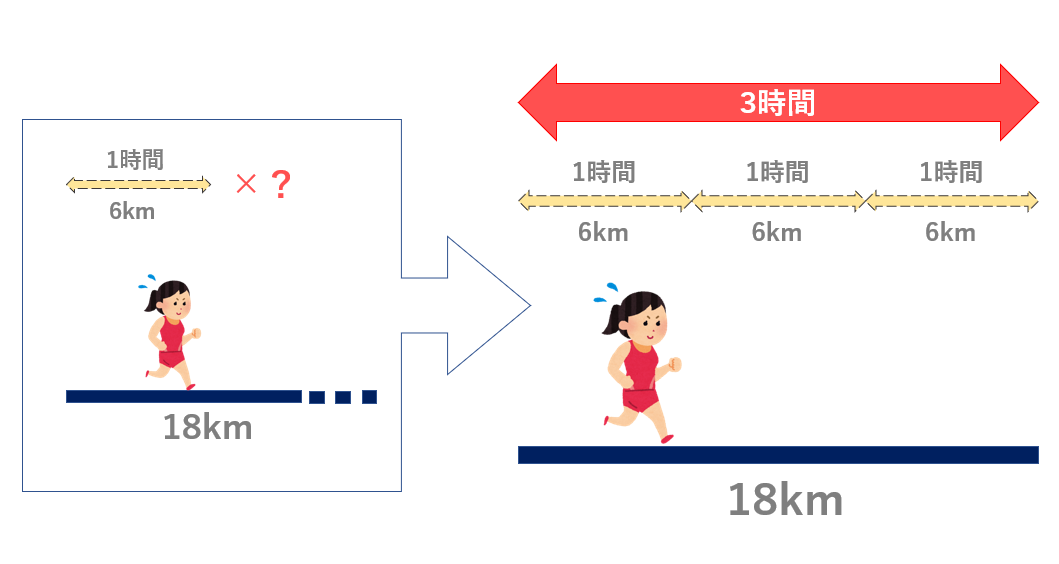



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社
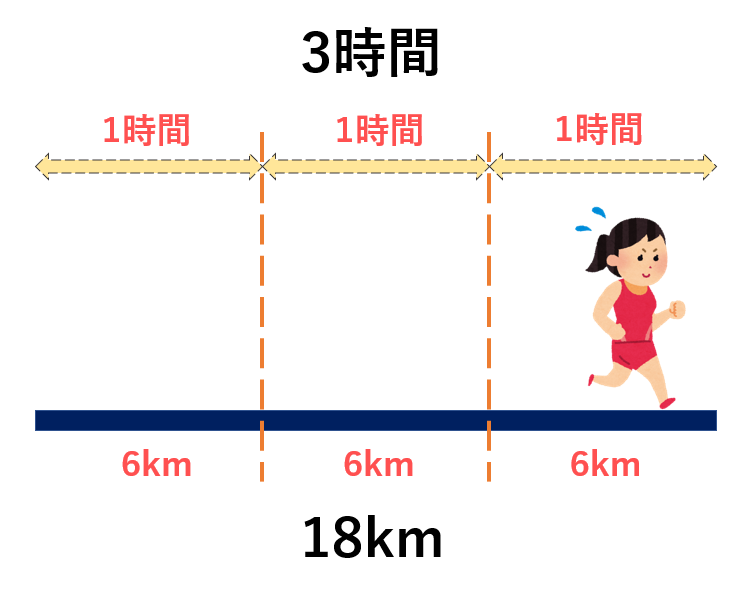



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社




波の表し方 波の基本式や波長と振動数と周期の求め方 Dr あゆみの物理教室




数基礎 Com 時速の求め方が分かる方法




音速の公式と計算 音は気温が1度上がるごとに秒速0 6mずつ速くなる 小学理科 Irohabook




表から速さを求める
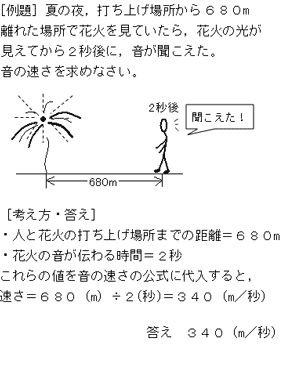



光 音 力 圧力 音の速さの求め方がわからない 中学生からの勉強質問 理科 進研ゼミ中学講座




等加速度直線運動の3公式の使い方がわかりません 理科 苦手解決q A 進研ゼミ高校講座
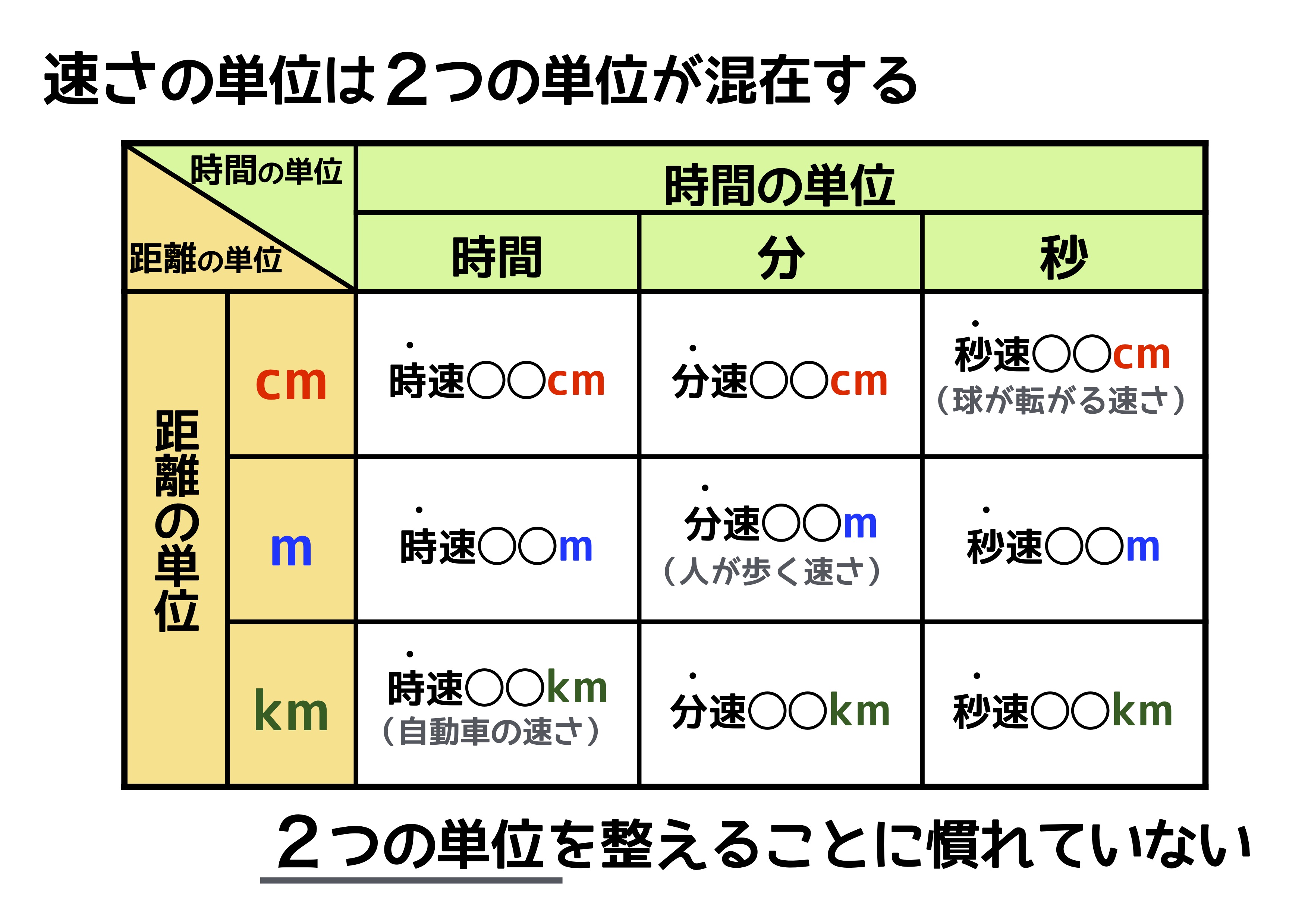



時速や分速の計算でミスをしないために 分数の約分利用の徹底を 中学受験ナビ



5年算数速さ 教え方のポイント
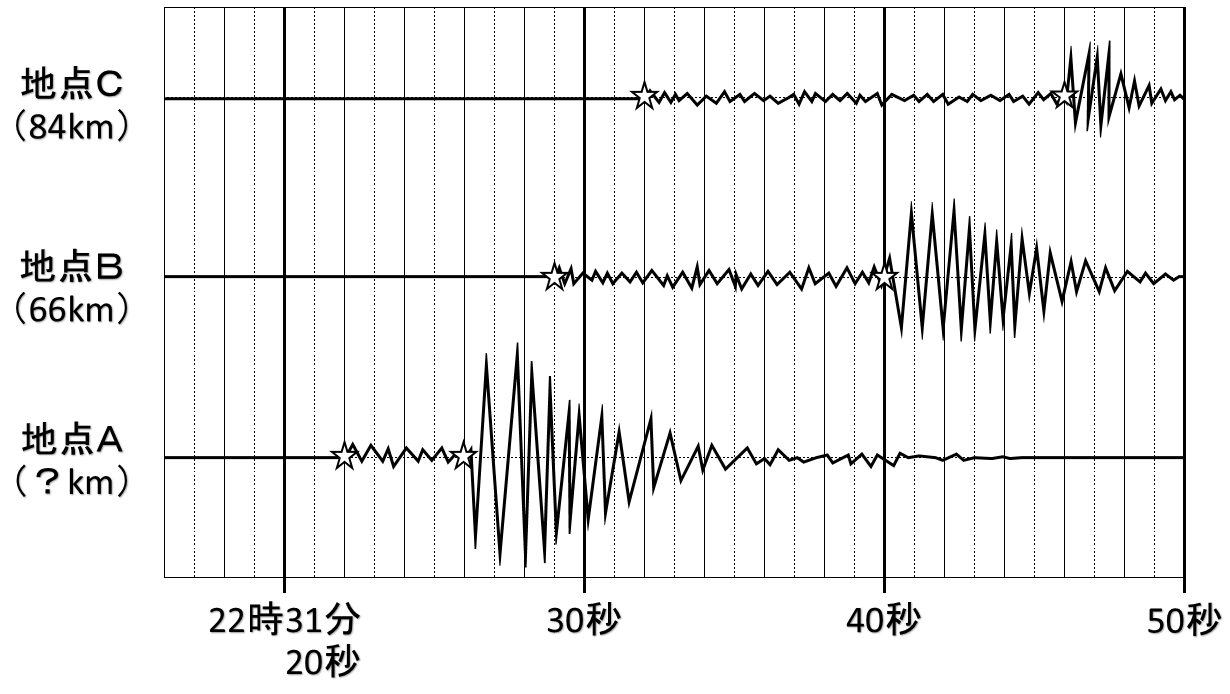



地震計の記録から速さを求める
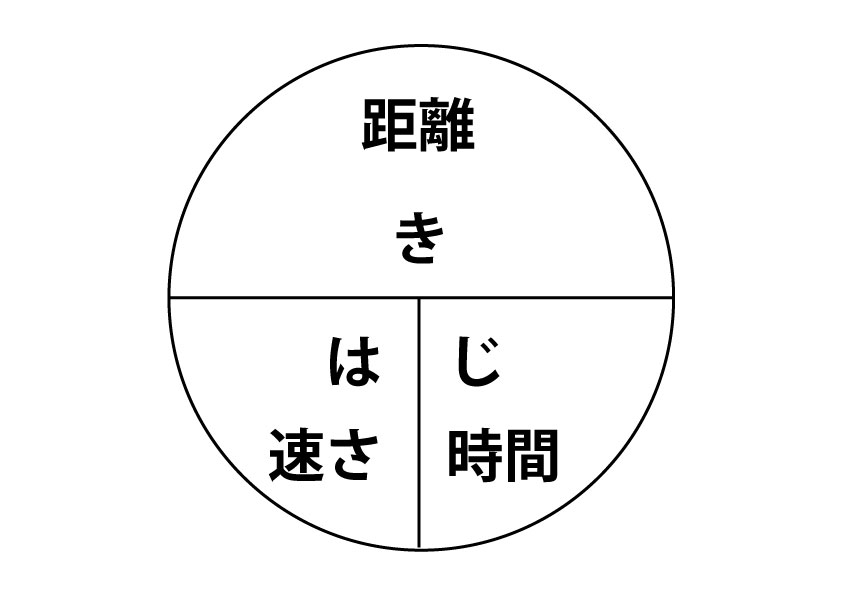



はじき みはじ の法則 速さ 時間 距離 簡単な公式の覚え方 Yattoke 小 中学生の学習サイト
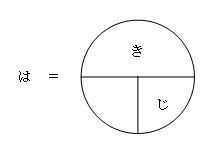



速さの求め方 もう一度やり直しの算数 数学
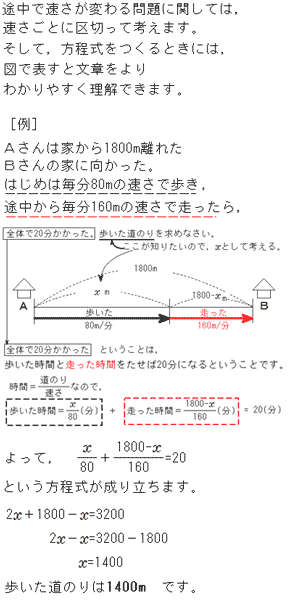



方程式 途中で速さが変わる問題の解き方 中学生からの勉強質問 数学 進研ゼミ中学講座
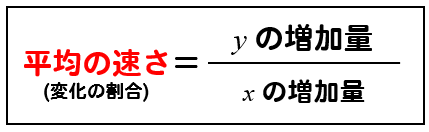



中3 数学 平均の速さの求め方を解説 数スタ
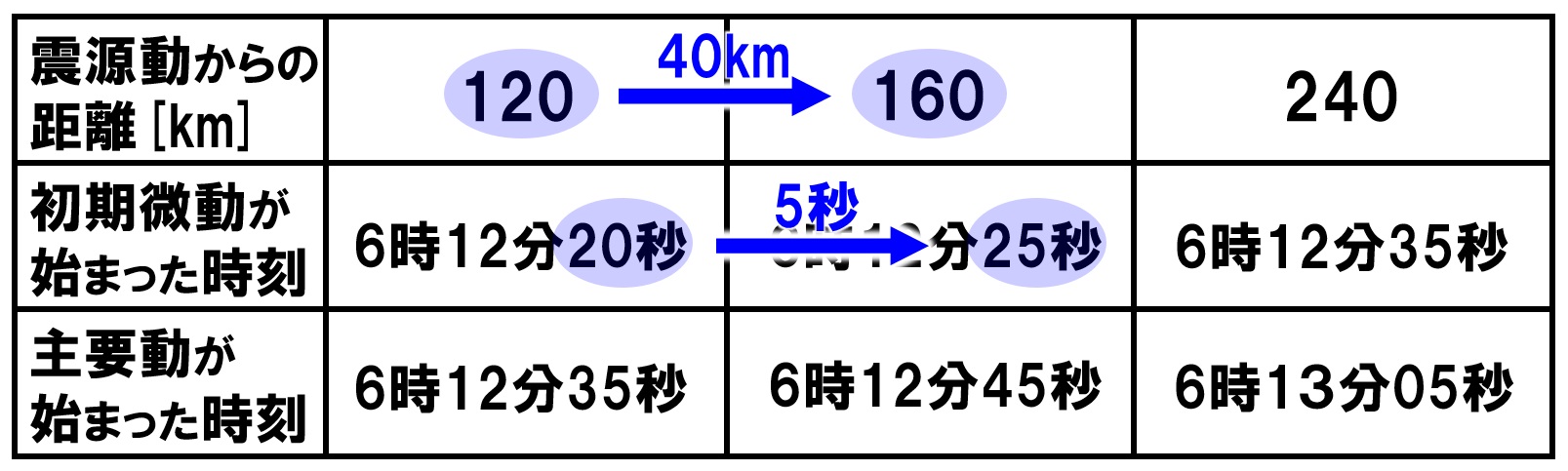



中1理科 地震の計算 テストや入試によく出る4パターン Pikuu




音速の公式と計算 音は気温が1度上がるごとに秒速0 6mずつ速くなる 小学理科 Irohabook




6年生算数ドリル 速さ
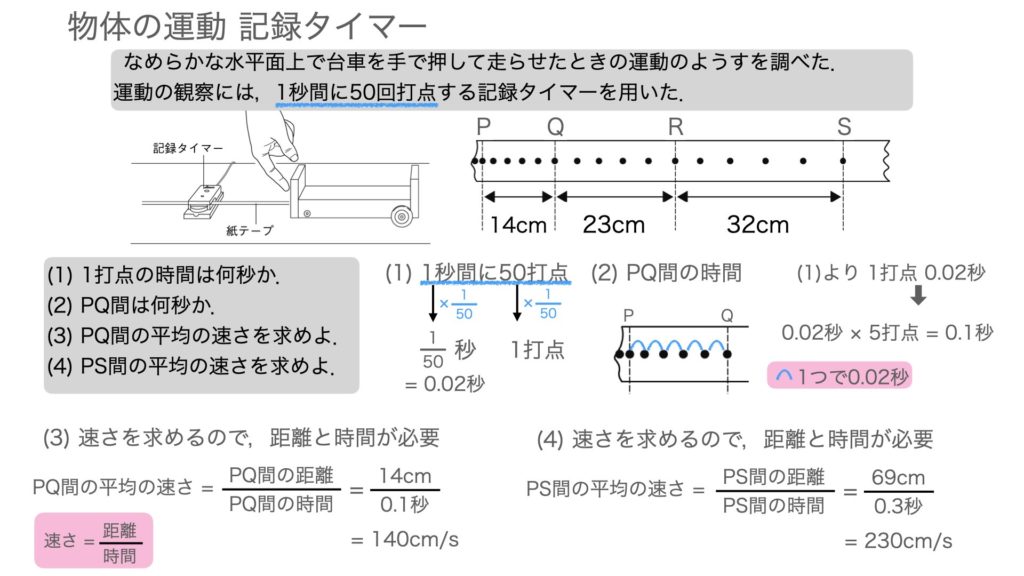



記録タイマーを使った物体の平均の速さの求め方 Hiromaru Note




音の速さの計算問題をくわしく解説




4 300 Km 2 4 Kmh Descubre Como Resolverlo En Qanda



1




加速度とは 直線運動をする物体の加速度 速度の求め方 高校生向け受験応援メディア 受験のミカタ




平均の速度と瞬間の速度の違いとは 公式および求め方




はじきの計算 例題を使って問題を解説 速さ 距離 時間を求める方法は 数スタ
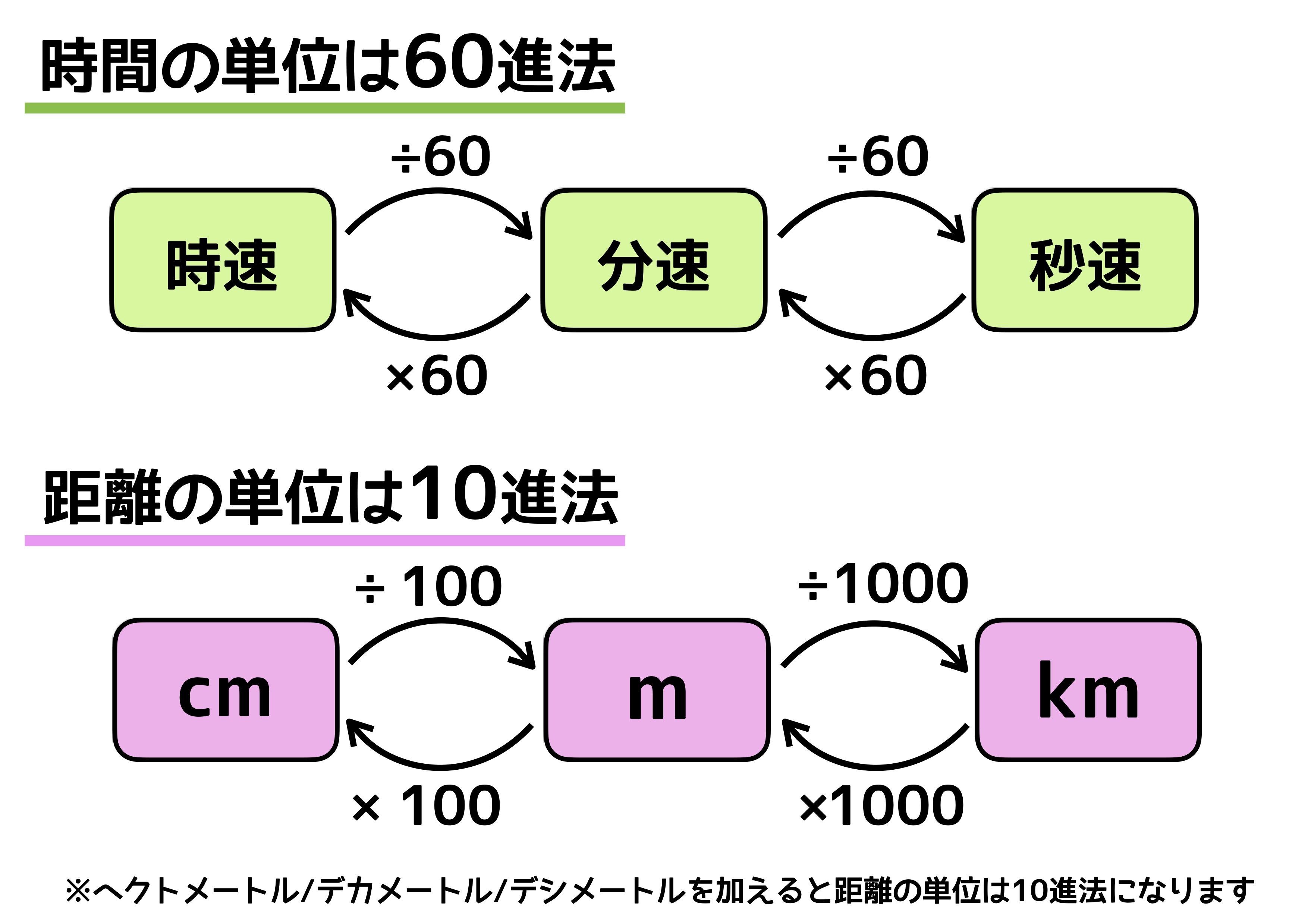



時速や分速の計算でミスをしないために 分数の約分利用の徹底を 中学受験ナビ




中1数学 文字で表すコツ4 速さ 時間 距離 練習編 映像授業のtry It トライイット
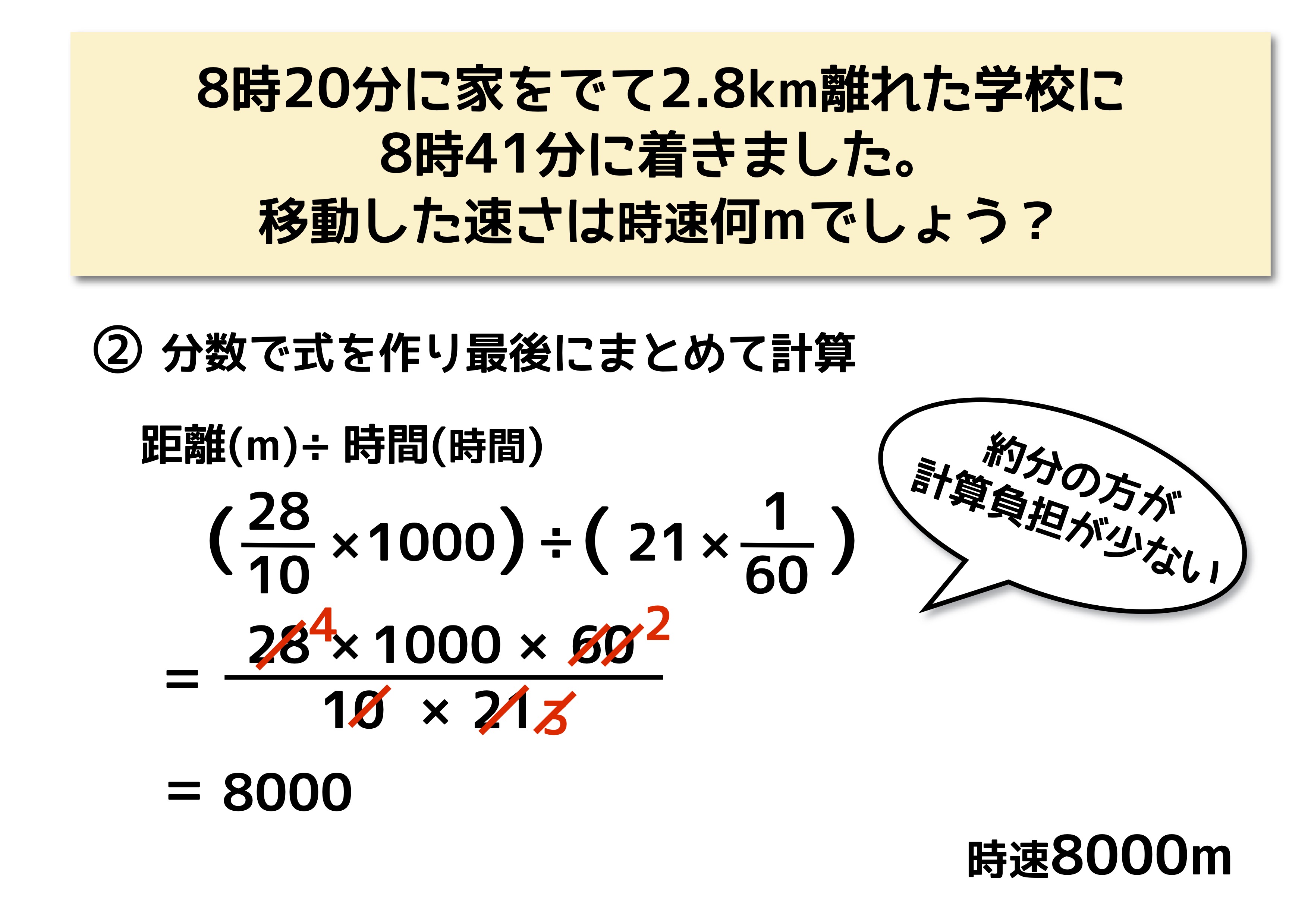



時速や分速の計算でミスをしないために 分数の約分利用の徹底を 中学受験ナビ




速さと時間から道のりを求める問題 家庭学習レシピ
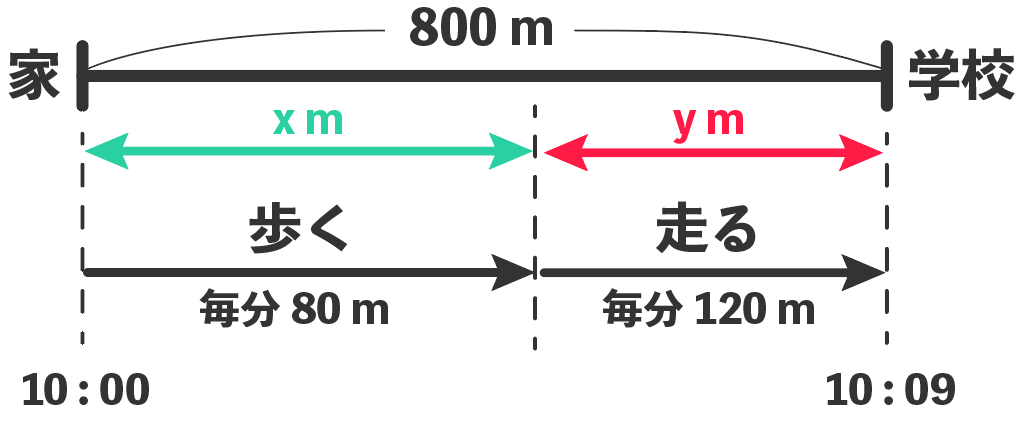



連立方程式の利用 速さ 道のり 時間の文章問題の解き方 Qikeru 学びを楽しくわかりやすく




速さ まとめ 小学生 算数のノート Clear




簡単な教え方が知りたい 小学6年生の算数 速度 の問題の解説法 もくもくサポート




しっかり区別しよう 平均の速度と瞬間の速さ 物理のいろは



1




速さ 分速と秒速 数学の記録




物理 平均の速さ 瞬間の速さ 厚木東 Youtube
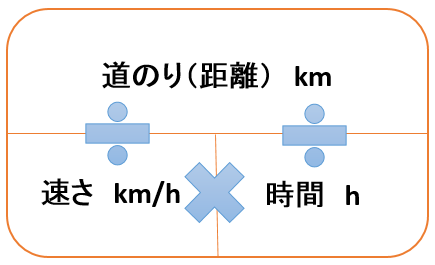



小中学生 道のり 速さ 時間の公式を理解しよう 偏差値40プログラマー
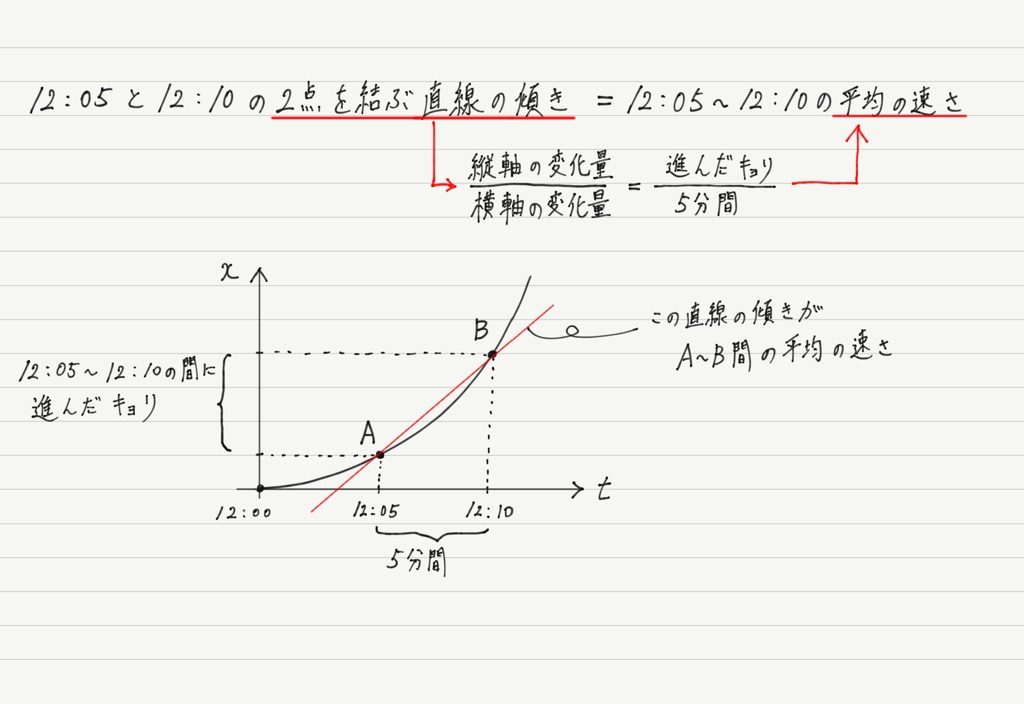



速度と加速度 平均と瞬間 高校物理をあきらめる前に 高校物理をあきらめる前に




往復の平均の速さ 間違えずに求められますか




小学生算数 間違いやすい平均速度の求め方 思い込みをなくす 偏差値40プログラマー



津波の速さはどれくらい




速さと運動 Ict教材eboard イーボード




速度と速さの違いって 速度を定義しよう 物理のいろは




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




すきるまドリル 小学6年生 算数 速さ 無料学習プリント すきるまドリル 無料学習プリント




Excel エクセルで距離 位置 と時間から速度計算をする方法 速さの求め方



5年算数速さ 教え方のポイント




分数と速さ 算数 数学が好きになりmath
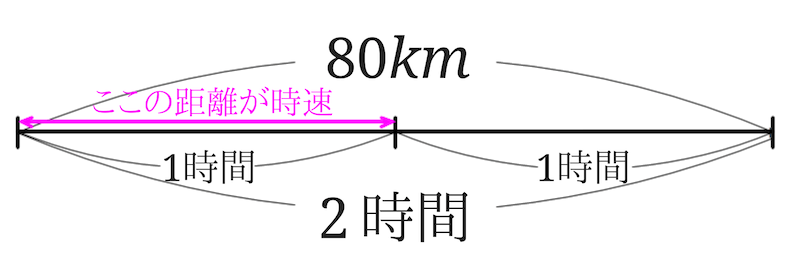



速さの求め方を時速 分速 秒速ごとに解説 みけねこ小学校




速さと時間から道のりを求める問題 家庭学習レシピ




往復の平均の速さ 間違えずに求められますか




速さ 時間の求め方 看護学校の受験数学 中学数学 を分かりやすく図解で説明 Kazアカデミー 大阪の看護学校 看護予備校
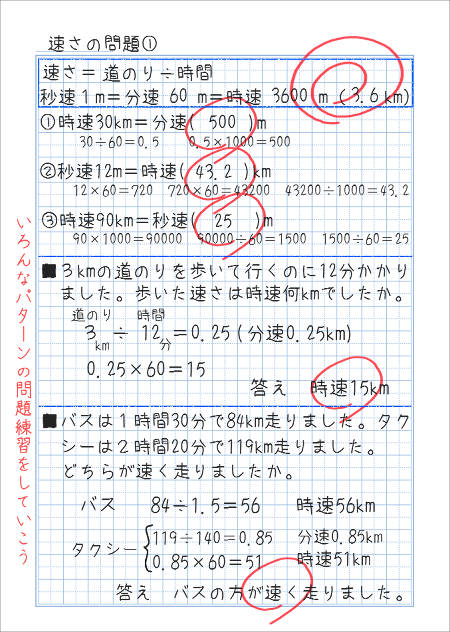



速さの問題 その1 家庭学習レシピ




速さの求め方を習う時に 問題文に出てくるいろいろなものの速さを 自分なりにイメージすることができれば 理解しやすいのではないかと思います たとえば 自分が歩く速さ 車の速さなど 学習ノート 学習 一生懸命に勉強する
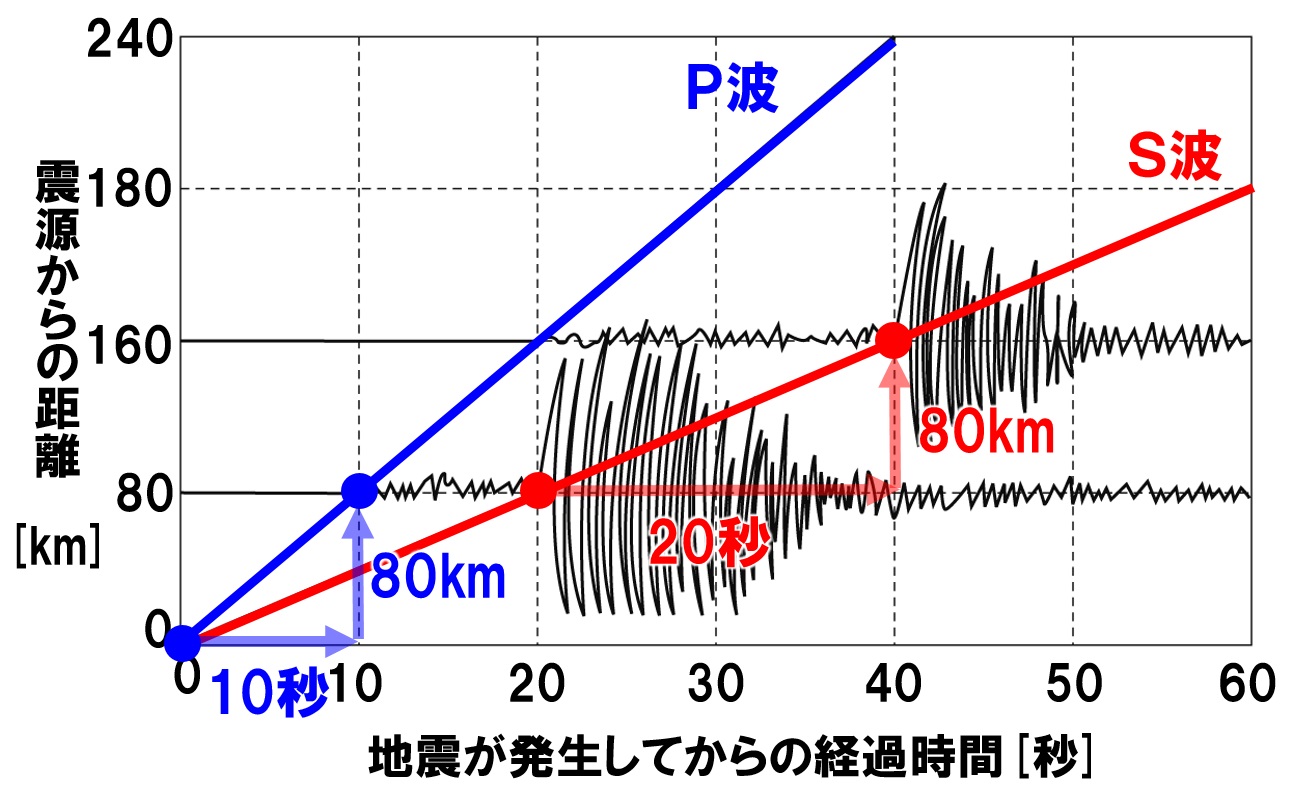



中1理科 地震の計算 テストや入試によく出る4パターン Pikuu




平均の速度と瞬間の速度の違いとは 公式および求め方




時速の求め方をおしえてください Clear




音の速さ 秒速でどれくらい 公式を確認しておこう 中学数学 理科の学習まとめサイト




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




速さ 時速 数学の記録
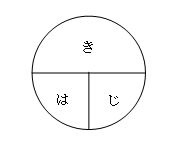



速さの求め方 もう一度やり直しの算数 数学
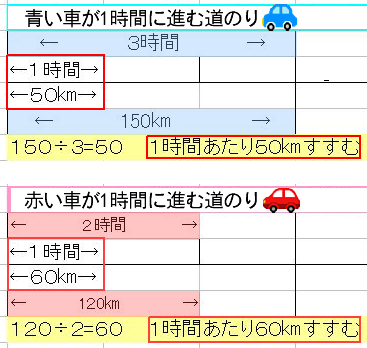



5年算数速さ 教え方のポイント
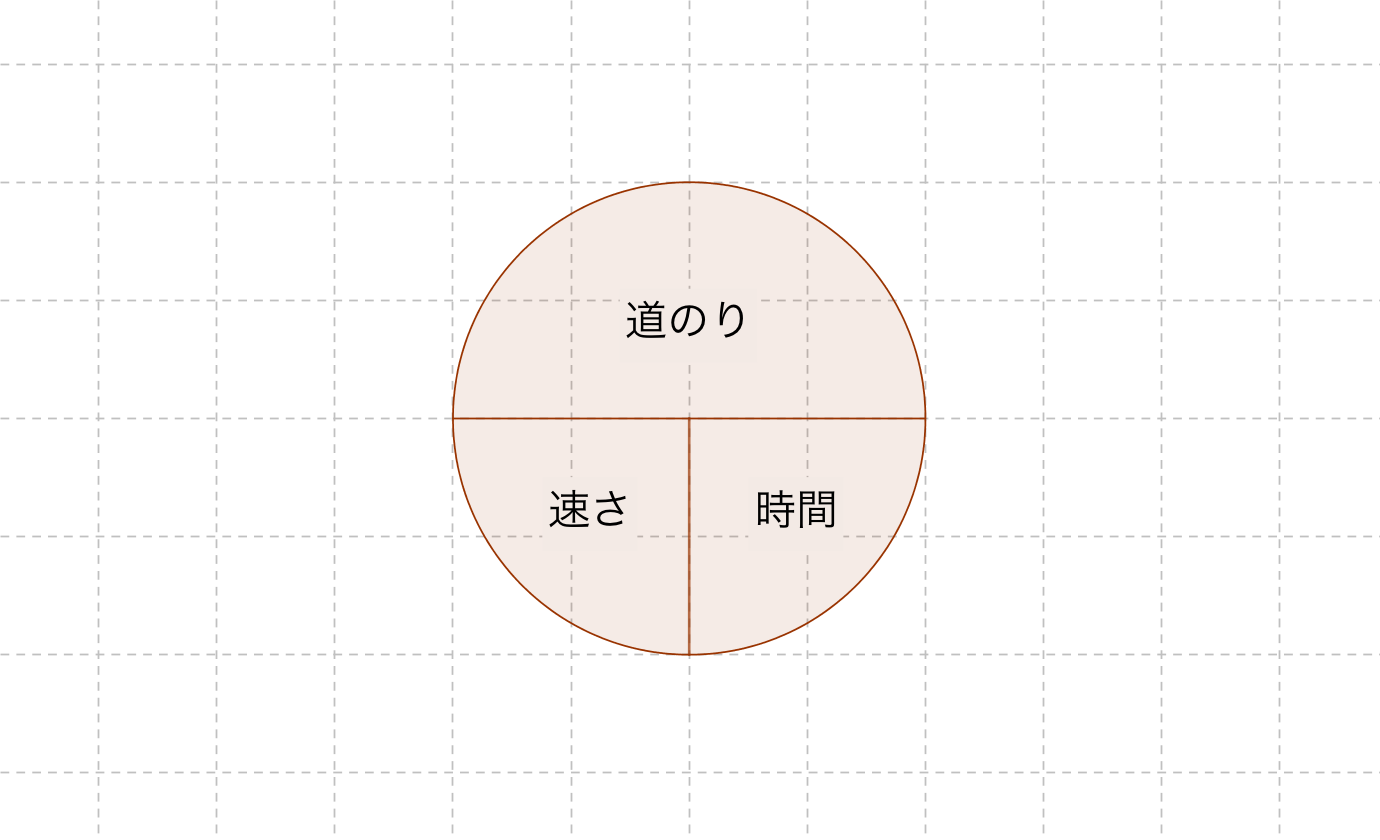



速さの公式 道のり 時間 算数の公式




理科の平均の速さはどうやって求めますか Clear
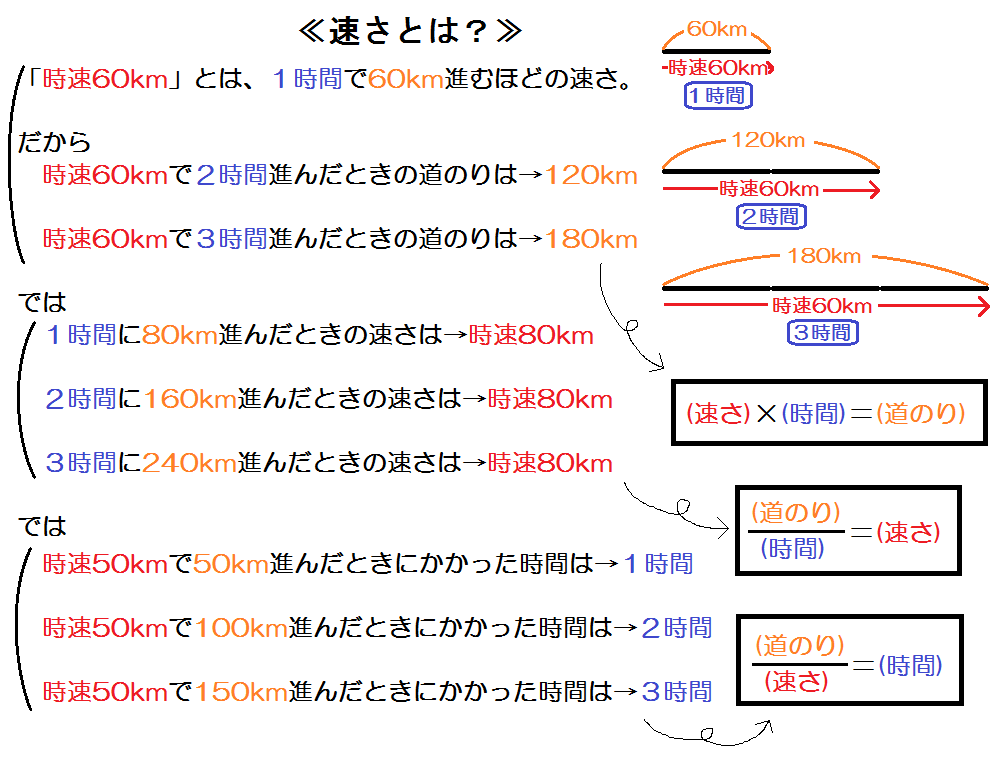



中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun



0 件のコメント:
コメントを投稿